奇函数与偶函数相乘的奥秘：函数乘积的对称性

奇函数与偶函数的乘积在数学分析中是一个经典且有趣的话题。奇函数和偶函数是基于它们自身的对称性定义的两类特殊函数。奇函数指的是满足条件f(-x) = -f(x)的函数，而偶函数则满足g(-x) = g(x)的条件。这两类函数不仅在数学理论中有重要地位，在实际应用中也有广泛的应用。

当我们将一个奇函数f(x)与一个偶函数g(x)相乘时，得到的新函数h(x) = f(x) * g(x)具有一定的性质。为了探究这个新函数的性质，我们可以从定义出发，来验证它是否为奇函数或偶函数。

首先，我们计算h(-x)的值：

\[h(-x) = f(-x) * g(-x)\]

由于f(x)是奇函数，所以有f(-x) = -f(x)；而g(x)是偶函数，所以有g(-x) = g(x)。将这两个等式代入上面的表达式中，可以得到：

\[h(-x) = (-f(x)) * g(x) = -(f(x) * g(x)) = -h(x)\]

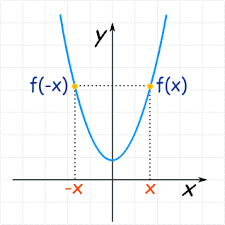
这表明，奇函数与偶函数的乘积h(x)也是一个奇函数。这是因为h(-x)的结果与-h(x)相等，满足奇函数的定义。

这个结论在数学上是非常有用的，因为它帮助我们理解了函数乘法的基本性质，并为我们提供了一种通过已知函数的性质来推导未知函数性质的方法。例如，在信号处理、物理问题建模等领域，这种性质的应用可以帮助我们简化复杂的问题，通过分解成更简单的奇函数和偶函数的乘积来解决。

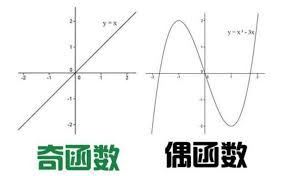
总之，奇函数与偶函数的乘积依然是一个奇函数。这一结论不仅加深了我们对奇函数和偶函数性质的理解，也为解决实际问题提供了新的视角和方法。